Modelagem da depressão e elaboração do diagrama LOOP simplificado via modelo Cusp Catástrofe Andr
- Grupo Psicologia
- 26 de jun. de 2019
- 9 min de leitura
Modelagem da depressão e elaboração do diagrama LOOP simplificado via modelo Cusp Catástrofe
Andrey Martioli, Gabriel Lima e Sergio Christoforo.
Resumo — Esse artigo consiste em lidar com a modelagem, no âmbito psicológico, da condição clínica conhecida como depressão. Para tal o modelo utilizado é o Cusp catástrofe que essencialmente é usado para tratar modelagens onde pequenas alterações circunstanciais causam mudanças repentinas. Assim, como quando foi desenvolvida na década de 1960 por René Thom e graças a esforços de Christopher Zeeman, consideramos um modelo em que a condição especial onde o equilíbrio pode ser identificado, é estável e existe uma função potencial bem definida - Função Lyapunov. Entre diversas variantes do método adotamos a modelo Butterfly. Ainda mais, a proposta consiste na elaboração de um diagrama de Loop simplificado e conhecimento das variáveis de estado que devem ser usadas para descrever o Fenômeno da depressão.
Palavras Chave — Modelo Butterfly, Modelagem psicológica, Depressão, Modelo simplificado, Diagrama de Loop.
I.Introdução
A depressão é uma condição patológica complexa que envolve tanto instabilidades biológicas quanto psicológicas. Essa condição afeta não somente a pessoa no seu contexto individual como também suas relações sociais em âmbitos familiares, escolares e profissional.
A depressão é conhecida por um dos seus traços mais marcantes que é a indução de uma completa inabilidade do indivíduo em realizar suas tarefas rotineiras. Segundo a APA - American Psychological Association - a depressão pode ser classificada como: "Um transtorno de humor que causa um sentimento persistente de tristeza e interesse. Afeta as capacidades de sentir, pensar e como o indivíduo se comporta podendo desencadear uma série de problemas físicos e emocionais. É recorrente a dificuldade em exercer atividades cotidianas e o sentimento de que a vida não vale a pena.".
Como descrito por Greenberg, P., Fournier, A., Sisitsky, T., Pike, C., & Kessler, R. no estudo “The economic burden of adults with major depressive disorder in the United States” publicado na revista de psiquiatria norte-americana é estimado que a depressão gere mais de 400 milhões de dias inábeis para pessoas com idade entre 15-44 anos ao longo de todo o território norte-americano e que o padrão é replicável ao longo de todo o globo.
As estimativas da APA sugerem que pelo menos 17 milhões de adultos norte-americanos sofreram durante pelo menos 1 ano com esse transtorno. Ou seja o montante pode chegar a mais de 6% de toda a população dos Estados Unidos da América.
Ainda existem casos críticos como mostrado por Richard Friedman, M.D. e Andrew Leon, Ph.D em uma publicação editorial para o "The New England Journal of Medicine" citam: “é seguro afirmar que entre 2,2% a 15% dos casos não tratados de depressão transcorrem a um caso de suicídio.” E complementam ressaltando que mesmo sem o fim trágico a doença é acompanhada de extremo sofrimento e prejuízo funcional ao indivíduo acometido.
Então, em uma ampla visão, essa doença trata-se de uma combinação de diversos fatores agregadores que podem levar a uma brusca mudança qualitativa no indivíduo que o afeta em diversas âmbitos. Fatores ambientais, genéticos, biológicos e psicológicos e físicos podem desencadear a depressão em pessoas distribuídas em um amplo espectro de idade. E mesmo que esses fatores sejam desfavoráveis devemos considerar outros como: Grandes traumas ou mudanças repentinas, stress e certas doenças psicológicas agravantes.
II.Abordagem no âmbito de sistemas dinâmicos
Como explicitado anteriormente a depressão é descrita por um espectro extremamente amplo. Pensando nisso, a utilização das ferramentas disponíveis para modelagem de sistemas dinâmicos se torna interessante. Segundo Daniel Herrera e Inge Bleijenbergh um ponto de vista sucinto para se tomar é encarar a depressão, do ponto de vista da modelagem, como uma “batalha” entre laços de reforço de um sistema LOOP. Ou seja, a partir de uma entrada, uma variável exógena, em uma variável inicial podemos analisar se o efeito dela, do ponto de vista do sistema, torna-se positivo ou negativo, acometendo mais ou então atenuando a condição de depressão inicial. A interação desses LOOPS nos leva a sistemas pouco comportados numericamente e portanto a uma modelagem onde breves alterações nas variáveis que descrevem nosso sistema podem mudar drasticamente a característica dele fazendo com que condições de equilíbrio existam ou não, conduzindo a repentinas e amplas alterações.
III.Fundamentação Teórica
A teoria do caos pode ser aplicada nas mais diversas áreas, desde a ecologia até a física, descrevendo diversos fenômenos. A grande vantagem nesse caso é que, do ponto de vista numérico, as funções pertencentes a essa metodologia conseguem descrever fenômenos mal comportados como os do nosso estudo.
Estudando a depressão podemos muitas vezes ser levados a crer que trata-se de um problema que enfrenta uma descontinuidade matemática dada a rápida mudança de caráter e demonstração dessa doença nos indivíduos, com variações abruptas de humor variando, desde um agradável sentimento de completude até a completa certeza de que não existe motivo algum para continuar vivo.
Essas amplas mudanças de no espectro visível não são, na maioria das vezes, acompanhadas por grandes a abruptas mudanças nas condições causadoras ou agregadoras. Essas condições, pelo contrário, variam de forma lenta e suave (Lorenz, 1967; Zeeman, 1976a).
O aparato matemático necessário para descrever a teoria da catástrofe é descrito no item seguinte.
Item 1 - Conceitos fundamentais da teoria da catástrofe
Diz-se que a função f:R^n → R tem um ponto crítico em ρ se
📷
Os pontos críticos de uma função são topologicamente importantes porque definem sua forma qualitativa e, portanto, o comportamento geral do fenômeno real que eles representam. O tipo de pontos críticos de uma função pode ser estabelecido pelo determinante da matriz hessiana, também conhecida como matriz de estabilidade:
📷
Se o fator determinante desta matriz não é nulo:
📷
nos pontos críticos ρ, então estes não são degenerados. Geometricamente falando, os pontos críticos não degenerados são o máximo, mínimo ou pontos de sela.
Ao aplicar o Teorema de Morse, esse tipo de função pode ser reduzida à forma quadrática:
📷
Onde λi são os autovalores da matriz de estabilidade e são conhecidos como funções Morse.
Quando a matriz de estabilidade é singular em um ponto crítico ou, isto é, quando:
📷
o ponto crítico é chamado de degenerado. Sob estas condições, se a teoria da catástrofe não se aplica, pouco pode ser dito sobre o comportamento da função em torno do ponto crítico. O teorema de Morse não é aplicável e, em princípio, não existe uma forma canônica à qual a função possa ser reduzida.
Os pontos críticos degenerados são de maior interesse, pois estão relacionados a instabilidades da função. Diz-se que uma função f: Rn-R é estruturalmente estável se para cada perturbação pequena o suficiente p:Rn-R, a função perturbada f + p mantém o mesmo número e tipo de pontos críticos que a função original f. Isto é, se houver um difeomorfismo que transponha f para f + p.
Em um sentido geométrico, isso significa que a função perturbada f + p mantém o mesmo número e tipo de pontos críticos que a função original f; isto é, que é qualitativamente o mesmo.
Funções com pontos críticos não degenerados, ou funções de Morse, são estruturalmente estáveis. Funções com pontos críticos degenerados são estruturalmente instáveis.
Quando a função representa um fenômeno físico, o conceito de instabilidade estrutural implica que o fenômeno real modelado pela função pode ser modificado significativamente com uma pequena perturbação.
De fato, em um fenômeno estruturalmente instável, vemos não apenas mudanças quantitativas, mas também mudanças qualitativas, sob pequenas perturbações.
Geralmente, uma função tem em sua maior parte pontos críticos não degenerados, dependendo dos valores de seus parâmetros e somente em alguns intervalos tem pontos críticos degenerados.
Para uma família de funções f: R^n x R^k→R, com n variáveis, chamadas variáveis de estado, e com parâmetros k, chamados parâmetros de controle, Thom estabeleceu a existência de formas canônicas se n≤2 e k≤5.
Essas formas canônicas são conhecidas como funções de catástrofe. A Tabela 1 mostra as funções de catástrofe elementares.
A condição:
📷
define a superfície de equilíbrio ou estado de cada função de catástrofe. Essas superfícies são de especial importância, uma vez que o comportamento de histerese e descontinuidade, entre outras peculiaridades, pode ser estabelecido e modelado nelas.
A figura 1 mostra a geometria da catástrofe em cúspide, onde as principais características dos fenômenos da catástrofe - histerese, bimodalidade, divergência e saltos repentinos - podem ser claramente observadas.
📷
Figura 1 : Geometría Cúspide Catástrofe. (a) superfície de equilíbrio, (b) corte transversal na superfície de equilíbrio.
📷
Item 2 - Cúspide Catástrofe Borboleta
Se mais de duas variáveis de estado determinam a resposta do sistema em questão acabamos recaindo sobre modelos mais complexos no âmbito da modelagem.
O modelo borboleta se debruça sobre problemas com quatro variáveis de controle e ainda mantém as mesmas propriedades do modelo simplificado da curva cúspide. Para essa modelagem temos a mais rica gama de espectros de aplicação (Zeeman, 1976a).
“Se d, é positivo, o espaço de resposta da borboleta parece muito com a superfície de resposta da cúspide exceto que em vez de ser dobrado sobre as curvas é dobrado ao longo de superfícies inteiras.
Variações no terceiro fator de controle, o fator de polarização, c, tem o efeito de mover a curva em forma de s para a direita e para baixo se c é negativo e para a esquerda e para cima se c for positivo, assumindo que a superfície de resposta superior esteja à direita, como na Fig. 1. A Fig. 2 mostra
isto para dois valores de c.
Em aplicações práticas, o viés significa que existem mudanças abruptas ou catástrofes no aspecto comportamental e são variáveis que ocorrem em diferentes valores enviesados de fatores normais de divisão ou conflito, dependendo do valor do fator determinante. Por exemplo, se houvesse valor negativo na variável de tendência, o fator normal precisaria aumentar muito mais antes que houvesse mudança catastrófica na variável resposta.” (Bryan R. Flay-1978)
📷
📷
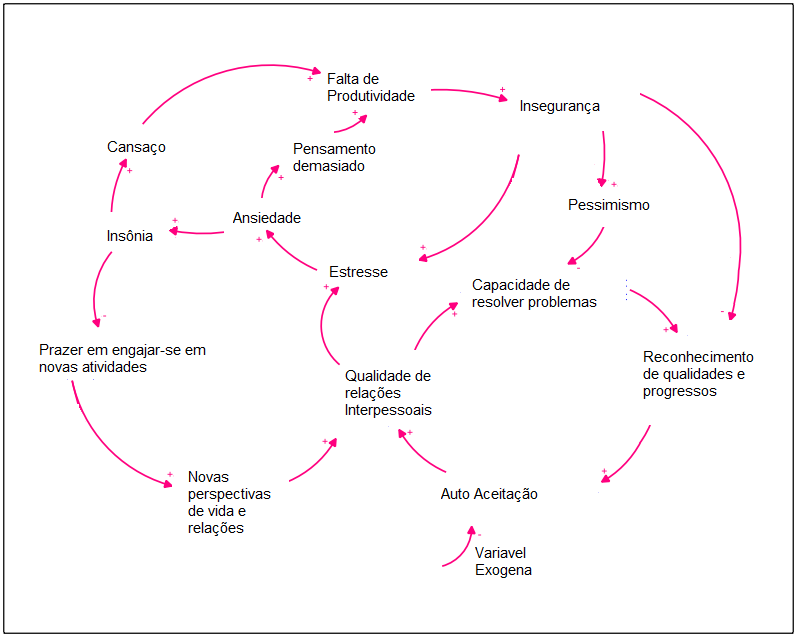
Item 3 - Diagrama de LOOP
Diagramas de LOOP consistem amplamente em uma análise qualitativa da relação entre as variáveis de estado e os efeitos disso para a variável resposta do sistema. A relação é descrita por setas que indicam o sentido do caminhar da perturbação no sistema e as interações podem receber sinal positivo ou negativo. O sinal é responsável por representar o efeito agregador ou atenuador de uma correlação.
Item 4 - Patient Health Questionnaire (PHQ)
O modelo PHQ-9 consiste em quantificar sentimentos de um paciente através de questionários para que assim facilite a análise quantitativa da depressão, é o caso que nos interessa. com perguntas feitas a um grande número de pessoas para que as mesmas dessem um valor de 0 - 1 pode-se ter um valor para estresse, insônia, ansiedade, baixa auto estima, tristeza entre outros.
este modelo visa o tratamento dos pacientes coletando suas informações antes e depois do tratamento, mas para esta análise coletamos os dados da seguinte tabela.
📷
que com esses valores aplicados para o estresse, insônia, relações interpessoais e ansiedade que foi aplicado no Cúspide Catástrofe Borboleta.
IV. Desenvolvimento
Item 1 - Diagrama LOOP
A um primeiro momento a abordagem qualitativa do problema se torna extremamente necessária para que tenhamos, em um prospecto inicial, o conhecimento das variáveis a serem tratadas pelo problema. Evidentemente, segundo Daniel Herrera e Inge Bleijenbergh,o primeiro passo é a elaboração do diagrama LOOP para representar o sistema estudado. O Diagrama é mostrado a seguir:
📷
Item 2 - Função Potencial
Como bem descrito no referencial teórico as funções catástrofe podem ser descritas como funções potências de Lyapunov amplamente difundidas na literatura. Para nosso caso temos a função potencial:
📷
Onde os controladores a,b,c e d representam as variáveis pivôs tratadas no diagrama LOOP e representam o comportamento único do sistema. Pequenas variações nessas variáveis afetam enormemente as características do nosso sistema.
Ainda sim recaimos sobre um problema, como quantificar as nossas variáveis pivô. No estudo conduzido por PHD. Rui Wang, “Tracking Depression Dynamics in College Students Using Mobile Phone and Wearable Sensing”, no qual nos baseamos amplamente para a quantificação, ele, por meio de aplicativos móveis, consegue contribuir largamente para a literatura envolvendo modelagem da depressão.
Utilizaremos então:
📷
Considerando passos de 0.05 analisamos ,via PHQ, o efeito agravado pela ampliação desses fatores no sistema.
📷
Em rápida análise é perceptível o efeito exponencial do agravamento das variáveis.
📷
O efeito característico de divergência confirma que tratamos de uma função potencial mal comportada numericamente. Retomamos a função potencial de Lyapunov:
📷
📷
Onde v e u surgem devido a representação da função potencial na forma paramétrica e são nada mais que o funções de a, b, c e d.
Em outras palavras, a função Lyapunov potencial é descrita como V(X,a,b,c,d).
Onde destaca-se a região de inacessibilidade
É interessante notar o comportamento dos pontos ao redor do pontos de catástrofe nas imagens que seguem:
📷
V. Conclusões
Neste artigo conseguimos abordar, sob um primeiro ponto de vista, a abordagem, no âmbito da modelagem de sistemas dinâmicos, adotada para que se compreenda o fenômeno conhecido como depressão. Ainda sim a solução de sistemas mal condicionados numericamente ainda é complexa e só é possível graças ao processamento computacional.
Isso mostra como a implementação dos algoritmos via MATLAB torna a tarefa mais simples. Para nossos sistemas mal-comportados numericamente é sempre dispendioso do ponto de vista de processamento a realização das tarefas. Ainda sim é visível que os modelos catástrofe são muito bem aplicados quando refere-se a modelagem da depressão. Como ferramenta de entendimento da modelagem de sistemas esse trabalho se mostrou importantíssimo permitindo um contato multidisciplinar e aplicado.
V. Referências
RUI WANG, “Tracking Depression Dynamics in College Students Using Mobile Phone and Wearable Sensing”.
“Cutting the Loops of Depression: a System Dynamics Representation of the Feedback Mechanisms Involved in Depression Development And Its Treatment”,Daniel Herrera and Inge Bleijenbergh
Zahler Sussman “Claims and accomplishments of applied catastrophe” - 27/10/1997
CATASTROPHE THEORY IN SOCIAL PSYCHOLOGY: SOME APPLICATIONS TO ATTITUDES AND SOCIAL BEHAVIOR' by Brian R. Flay
Friedman, R.A. & Leon, A.C. (2007). NEJM — Expanding the Black Box — Depression, Antidepressants, and the Risk of Suicide. New England Journal of Medicine, 356:2343-2346
https://psychcentral.com/blog/the-black-box-warning-antidepressants-and-the-risk-of-suicide/
https://www.apa.org/topics/depression/recover
https://www.nimh.nih.gov/health/topics/depression/index.shtml#part_145396
Greenberg, P., Fournier, A., Sisitsky, T., Pike, C., & Kessler, R. (2005 and 2010). The economic burden of adults with major depressive disorder in the United States. Journal of Clinical Psychiatry 76, 155-162.
Kim, Yeon Hee; Kim, Hwa Jung; Ahn, Seound Do; Seo, Yun Jeong; Kim, So Hee (2013). Effects of meditation on anxiety, depression, fatigue, and quality of life of women undergoing radiation therapy for breast cancer. Complementary Therapies in Medicine 21: 379-387
McGinn, LK, Cukor, D, & Sanderson, WC (2005). The relationship between parenting style, cognitive style, and anxiety and depression: Does increased early adversity influence symptom severity through the mediating role of cognitive style? Cognitive Therapy and Research, 29, 219-242.
Zeeman, E. C. Catastrophe theory. Sci. Amer.. 1976 234 (4),65-83. (a) Zeeman, E. C. A mathematical model for conflicting judgments caused by stress, applied to possible misestimations of speed caused by alcohol. Brit. j. math. stat. PsychoZ., 1976,29,19-31. (b)



Comentários